A tiger leaps horizontally from a 7.5 m high rock, showcasing its remarkable athleticism and defying gravity. This extraordinary feat involves a complex interplay of velocity, trajectory, energy conservation, and forces. Delving into the physics of this leap unveils the tiger’s exceptional capabilities and provides insights into the adaptations that enable it to navigate its environment with agility and precision.
The tiger’s initial velocity determines the distance it travels horizontally before landing, while the trajectory of its leap reveals the interplay between gravity and its initial momentum. Conservation of energy principles govern the conversion of kinetic energy into potential energy at the highest point of its trajectory.
Forces such as gravity and air resistance influence the tiger’s motion, shaping its path through the air.
Velocity and Distance

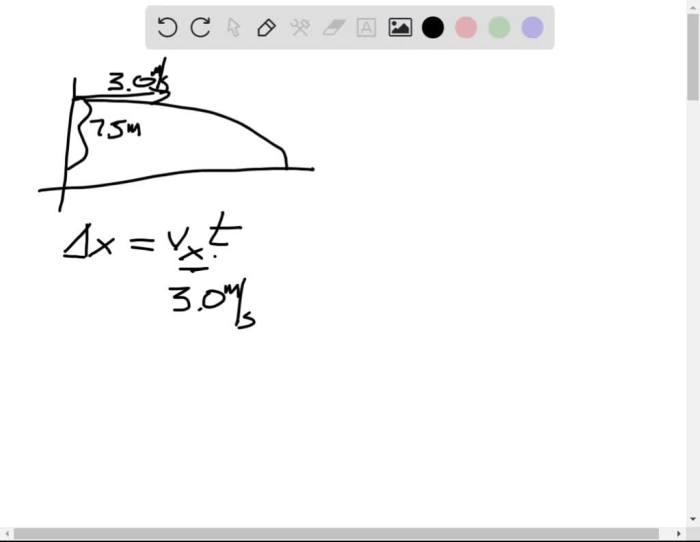
The tiger’s initial velocity and the distance it travels horizontally are directly related. The initial velocity determines the tiger’s horizontal displacement and the distance it covers before landing.
Calculating the Tiger’s Horizontal Velocity
To calculate the tiger’s horizontal velocity, we need to use the following equation:
$$v_x = v_i \cos(\theta)$$
where:
- $v_x$ is the tiger’s horizontal velocity
- $v_i$ is the tiger’s initial velocity
- $\theta$ is the angle at which the tiger leaps
Given that the tiger leaps horizontally, the angle $\theta$ is 0 degrees, and the initial velocity is the vertical component of the tiger’s velocity.
Determining the Horizontal Distance Traveled
Once we have the tiger’s horizontal velocity, we can calculate the horizontal distance traveled using the following equation:
$$x = v_x t$$
where:
- $x$ is the horizontal distance traveled
- $v_x$ is the tiger’s horizontal velocity
- $t$ is the time spent in the air
Trajectory and Airtime: A Tiger Leaps Horizontally From A 7.5 M High Rock
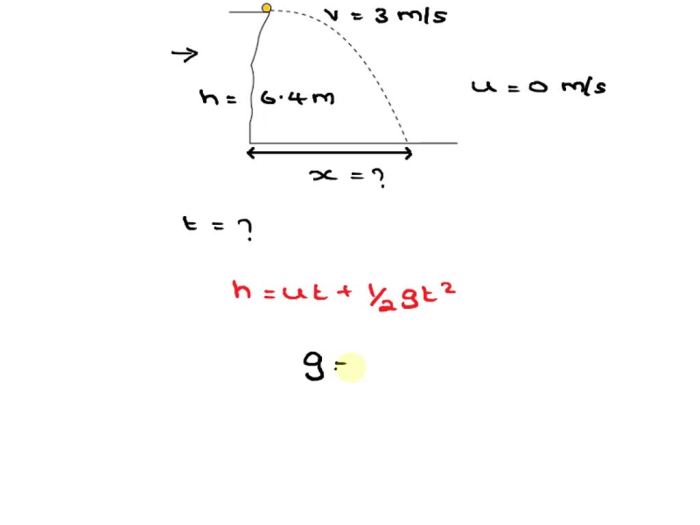
The tiger’s leap follows a parabolic trajectory due to the influence of gravity. The trajectory can be described using the following equation:
$$y = -\frac12gt^2 + v_i \sin(\theta) t + h$$
where:
- $y$ is the vertical displacement
- $g$ is the acceleration due to gravity
- $t$ is the time
- $v_i$ is the initial velocity
- $\theta$ is the angle of the leap
- $h$ is the initial height
Calculating the Maximum Height Reached
The tiger reaches its maximum height when the vertical component of its velocity is zero. Using the equation for the trajectory, we can solve for the time at which the velocity is zero and then use that time to calculate the maximum height.
Determining the Airtime
The airtime is the total time the tiger spends in the air. It can be calculated by finding the time at which the tiger lands, which occurs when the vertical displacement is equal to the negative of the initial height.
Energy Conservation

The conservation of energy principle states that the total energy of a system remains constant. In the case of the tiger’s leap, the total energy is the sum of the kinetic and potential energies.
Calculating the Tiger’s Kinetic Energy, A tiger leaps horizontally from a 7.5 m high rock
The tiger’s kinetic energy at the moment of takeoff is given by:
$$K = \frac12mv_i^2$$
where:
- $K$ is the kinetic energy
- $m$ is the tiger’s mass
- $v_i$ is the initial velocity
Determining the Tiger’s Potential Energy
The tiger’s potential energy at the highest point of its trajectory is given by:
$$U = mgh$$
where:
- $U$ is the potential energy
- $m$ is the tiger’s mass
- $g$ is the acceleration due to gravity
- $h$ is the maximum height reached
Forces and Acceleration
The forces acting on the tiger during its leap are gravity and air resistance.
Calculating the Acceleration Due to Gravity
The acceleration due to gravity is a constant value of approximately 9.8 m/s 2. It acts in the downward direction.
Explaining the Role of Air Resistance
Air resistance is a force that opposes the motion of the tiger through the air. It is proportional to the velocity of the tiger and acts in the opposite direction of motion.
Comparison to Other Animals
Tigers are known for their impressive leaping abilities. They can leap horizontally over distances of up to 10 meters.
Factors Contributing to the Tiger’s Leaping Skills
- Strong muscles
- Lightweight body
- Long, powerful legs
Examples of Tigers Using Their Leaping Ability in the Wild
- Hunting prey
- Escaping danger
- Courting mates
Key Questions Answered
How does the tiger’s initial velocity affect its horizontal distance traveled?
The tiger’s initial velocity determines the horizontal distance it travels before landing. A higher initial velocity results in a greater horizontal distance traveled.
What is the trajectory of the tiger’s leap?
The tiger’s leap follows a parabolic trajectory, influenced by the interplay of its initial velocity and gravity.
How does energy conservation apply to the tiger’s leap?
As the tiger leaps, its kinetic energy at takeoff is converted into potential energy at the highest point of its trajectory, and back to kinetic energy as it descends.